FIG. 2 shows a block schematic diagram of a steganographic encoder of the present invention.
13 June 2003
[Federal Register: June 13, 2003 (Volume 68, Number 114)] [Notices] [Page 35392] From the Federal Register Online via GPO Access [wais.access.gpo.gov] [DOCID:fr13jn03-63] ----------------------------------------------------------------------- DEPARTMENT OF DEFENSE Department of the Army Availability of a Novel Steganography Technology for Exclusive, Partially Exclusive, or Non-Exclusive Licenses AGENCY: Department of the Army, DOD. ACTION: Notice of availability. ----------------------------------------------------------------------- SUMMARY: The Department of the Army announces the general availability of exclusive, partially exclusive, or non-exclusive licenses relative to a novel stenography technology as described in U.S. Patent ``Spread Spectrum Image Steganography'' (U.S. Patent No. 6,557,103), April 29, 2003; Marvel, et al. Any license shall comply with 35 U.S.C. 209 and 37 CFR 404. FOR FURTHER INFORMATION CONTACT: Michael D. Rausa U.S. Army Research Laboratory, Office of Research and Technology Applications, ATTN: AMSRL-DP-T/Bldg., 459, Aberdeen Proving Ground, MD 21005-5425, telephone: (410) 278-5028. SUPPLEMENTARY INFORMATION: None. Luz D. Ortiz, Army Federal Register Liaison Officer. [FR Doc. 03-15018 Filed 6-12-03; 8:45 am] BILLING CODE 3710-08-M
| United States Patent | 6,557,103 |
| Boncelet, Jr. , et al. | April 29, 2003 |
The Spread Spectrum Image Steganography (SSIS) of the present invention is a data hiding/secret communication steganographic system which uses digital imagery as a cover signal. SSIS provides the ability to hide a significant quantity of information bits within digital images while avoiding detection by an observer. The message is recovered with low error probability due the use of error control coding. SSIS payload is, at a minimum, an order of magnitude greater than of existing watermarking methods. Furthermore, the original image is not needed to extract the hidden information. The proposed recipient need only possess a key in order to reveal the secret message. The very existence of the hidden information is virtually undetectable by human or computer analysis. Finally, SSIS provides resiliency to transmission noise, like that found in a wireless environment and low levels of compression.
| Inventors: | Boncelet, Jr.; Charles G. (Newark, DE); Marvel; Lisa M. (Churchville, MD); Retter; Charles T. (Belcamp, MD) |
| Assignee: | The United States of America as represented by the Secretary of the Army (Washington, DC) |
| Appl. No.: | 257136 |
| Filed: | February 11, 1999 |
| Current U.S. Class: | 713/176; 713/165; 713/181; 713/200; 713/201 |
| Intern'l Class: | G06F 011/30 |
| Field of Search: | 713/165,181,200,201,176 |
| 5636292 | Jun., 1997 | Rhoads. | |
| 5687236 | Nov., 1997 | Moskowitz et al. | |
| 5710834 | Jan., 1998 | Rhoads. | |
| 5745569 | Apr., 1998 | Moskowitz et al. | |
| 5745604 | Apr., 1998 | Rhoads. | |
| 5748763 | May., 1998 | Rhoads. | |
| 5748783 | May., 1998 | Rhoads. | |
| 5768426 | Jun., 1998 | Rhoads. | |
| 5822432 | Oct., 1998 | Moskowitz et al. | |
| 5822436 | Oct., 1998 | Rhoads. | |
| 5832119 | Nov., 1998 | Rhoads. | |
| 5841886 | Nov., 1998 | Rhaods. |
Schneier, Applied Cryptography, 1995, second edition, secs. 1.2, 8.4-8.6, 8.10, 9.12).* D. Kahn, The Code breakers--The story of secret writing. Scribner, New York, NY, 1967. B. Pfitzmann, Trials of Traced Traitors. In R. Anderson, editor, Information Hiding, First International Workshop. Lecture Notes in Computer Science, pp. 49-64. Spriknger-Verlag, Berlin, 1996.
C. Osborne R. Van Schyndel, A Tirkel. A digital watermark. Proceedings of
the IEEE International Conference on Image Processing 2:86-90, 1994. R.B. Wolfgang and E.J.Delp. A watermark for digital images. Proceedings of the IEEE International Conference on Image Processing, Lausanne, Switzerland, III:219-222, Sep. 1996. E. Milbrandt. Http://members.iquest.net/.about.mrmil/stego.html, Oct. 1997. Steganography Info and Archive. T. Leighton, I.J. Cox, J. Kilian and T. Shamoon. Secure Spread Spectrum Watermarking for Images, Audio and Video. Proceedings of the IEEE International Conference on Image Processing, Lansanne, Switzerland, III:243-246, Sep. 1996. C.I. Podilchuk and W. Zeng. Digital Image Watermarking Using Visual Models. In B.E. Rogowitz and T.N. Pappas, editors, Human Vision and Electronic Imaging II. vol. 3016, pp. 100-111. SPIE , Feb. 1997. B. Zhu, M.D. Swanson and A.H. Tewfik. Transparent Robust Image Watermarking. Proceedings of the IEEE International Conference on Image Processing, Lansanne, Switzerland, III:211-214, Sep. 1996. N. Moirimoto, W. Bender, D. Gruhl and A. Lu. Techniques for Data Hiding. IBM Systems Journal 35 (3&4), 1996. B. Zhu, M.D. Swanson and A.H. Twfik. Robust Data Hiding for Images. Proceeding sof the IEEE Digital Sinal Processing Workshop, Loen, Norway, pp. 37-40, Sep. 1996. M.D. Swanson and A.h. Twfik. Data Hiding for Multimedia Personalization, Interaction, and Protection. IEEE Signal Processing Magazine, 14(4);41-44, Jul. 1997. Y. Nakamura K. Tanaka and K. Matsui. Embedding Secret Information into a Dithered Multilevel Image. Proceedings of the IEEE military Communications Conference, Monterey, CA, pp. 216-220, 1990. E. Adelson, Digital Signal Encoding and Decoding Apparatus. U.S. patent 4,939,515, 1990. G.B. Rhoads. Steganography Method Employing Embedded Calibration Data. U.S. Patent 5,636,292, 1997. M. Coopeerman. Steganographic Method and Device. U.S. Patent 5,613,004, 1997. A.K. Jain. Fundamentals of Digital Image Processing. Prentice-Hall, Inc., Englewood Cliffs, NJ 1989. R.A. Scholtz, M.K. Simon, J.K. Omura and B.K. Levitt. Spread Spectrum Communications, vol. L Computer Science Press, Rockville, Maryland 1985. B. Schneier. Applied Cryptography--Protocols, Algorithms, and Source Code in C. John Wiley and Sons, Inc. New York, NY 1996. F. Hartung and B. Girod. Fast Public Key Watermarking of Compressed Video. Proceedings of the IEEE International Conference on Image Processing, Santa Barbara CA Oct. 1997. M. Abramowitz and I.A. Stegun. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications, Inc., New York, NY 1964. D.L. Donoho. De-noising by Soft-thresholding IEEE Transactions on Information Theory, 41(3):613-627, 1995. J.S. Lim. Two-Dimensional Signal and Image Processing. Prentice-Hall, Inc., Englewood Cliffs, NJ 1990. J.S. Lee. Digital Image Enhancement and Noise Filtering by Use of Local Statistics. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2:165-168, Mar. 1980. C.T. Retter. Decoding Binary Expansions of Low-rate Reed-Solomon Codes Far Beyond the BCH Bound. Proceedings of the 1995 IEEE International Symposium on Information Theory, Whistler, British Columbia, p. 276, Sep. 1995. M. Bossert and F. Hergert. Hard-and-Soft-Decision Decoding Beyond the Half Minimum Distance-an Algorithm for Linear Codes. IEEE Transactions on Information Theory, 32(5):709-714, Sep. 1986. J. Bee Bednar and Terry L. Watt. Alpha-Trimmed Means and Their Relationship to Median Filters. IEEE Transactions on Acoustics, Speech and Signal Processing, vol. ASSP-32 No. 1, pp. 145-153, Feb. 1984. L.J. Harcke and G.E. Wood. Laboratory and Flight Performance of the Mars Pathfinder (15,1/6) Convolutionally Encoded Telemetry Link. National Aeronautics and Space Administration (NASA), NASA/JPL TDA Progress Report 42-129, NASA Code 624-04-00MN-20, May 1997. A. J. Viterbi, Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm, IEEE, Transactions on Information Theory, Apr. 1967, vol. 1T-13 No. 2, pp. 260-269. |
Primary Examiner: Peeso; Thomas R.
Attorney, Agent or Firm: Kelly; Mark, Randolph; William W.

FIG. 2 shows a block schematic diagram of a steganographic encoder of the
present invention.

FIG. 3 shows a block schematic diagram of a steganographic decoder of the
present invention.

FIG. 4 shows a flow chart of the piece-wise linear modulation scheme of the
present invention.

FIG. 5 shows a graph comparing the pixel intensity and location of an original
cover image to the stegoimage.

DETAILED DESCRIPTION
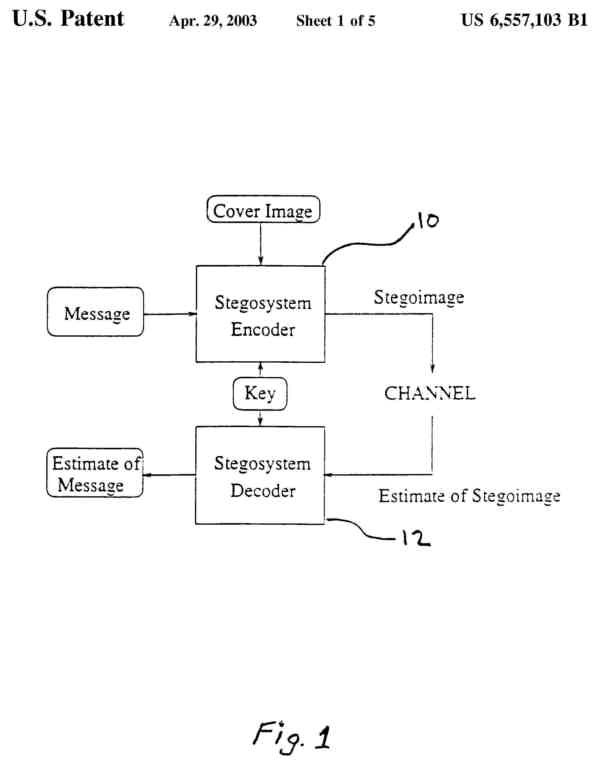
A block diagram of an image steganographic system is depicted in FIG. 1.
A message is embedded in a digital signal such as a signal representing a
digital image, by the stegosystem encoder 10 which uses numeric keys or
passwords. The resulting stegosignal, i.e., the stegoimage, is transmitted
in some fashion over a channel to an intended recipient where it is processed
by the stegosystem decoder 12 using the same key. During transmission the
stegoimage may be monitored by viewers who will notice only the transmittal
of the innocuous image without discovering the existence of the hidden message.
Techniques of spread spectrum communication, error control coding, and image
processing are combined to accomplish SSIS. The major processes of the
stegosystem encoder 10 are portrayed in FIG. 2. The message, after optional
encryption 20 with key 1, is encoded via an error correcting code 22 producing
the encoded message, m. The sender enters key 2 into a wideband pseudorandom
noise generator 24, generating a spreading sequence, n. Subsequently, the
modulation scheme 26 is used to spread the narrowband spectrum of m with
the spreading sequence n, thereby composing the embedded signal, s, which
is then input into an interleaver 28. The operation of the interleaver 28
may be dictated by key 3. The interleaved signal is now combined with the
cover image, to produce the stegoimage g which has been appropriately quantized
by quantizer 30 to preserve the initial dynamic range of the cover image.
The stegoimage is then transmitted in some manner to the recipient.
At the receiver, the stegosystem decoder 12, shown in FIG. 3, uses an image
restoration filter 40 followed by deinterleaving module 42 to construct an
estimate of the embedded signal s from the received stegoimage g. The recipient,
maintaining the same key 2 as the sender, replicates the spreading sequence
n with pseudorandom noise generator 44. The encoded message is then demodulated
at demodulator 46 with the spreading sequence, and an estimate of the encoded
message, m is constructed. The estimate of the message is then decoded via
the error correcting decoder 48, optionally decrypted at decrypter 50, and
revealed to the recipient.
The ability of SSIS to hide information is due to the existence of noise
encountered during image acquisition. SSIS uses inherent noise to hide
information within the digital image. Since wideband thermal noise, inherent
to imagery of natural scenes captured by photoelectronic systems, can be
modeled as additive white Gaussian noise (AWGN) this type of noise is included
in the SSIS system. SSIS is able to mimic this inherent noise to hide the
secret information within the digital image. In other types of coherent imaging,
the noise can be modeled as speckle noise {17}, which is produced by coherent
radiation from the microwave to visible regions of the spectrum. The concepts
of SSIS can be extended to imagery with other noise characteristics than
those modeled by AWGN. The additional noise which conceals the hidden message
is a natural phenomenon of the image and therefore, if kept at typical levels,
is not perceived by the casual observer or detectable by computer analysis.
Spread spectrum communication is the process of spreading the bandwidth of
a narrowband signal across a wide band of frequencies. This can be accomplished
by modulating the narrowband waveform with a wideband waveform, such as white
noise. After spreading, the energy of the narrowband signal in any one frequency
band is low and therefore difficult to detect. SSIS uses a variation of this
technique to embed a message, typically a binary signal, within samples of
a low power white Gaussian noise sequence consisting of real numbers. The
resulting signal, perceived as noise, is then added to the cover image to
produce the stegoimage. Since the power of the embedded signal is much lower
compared to the power of the cover image, the SNR is also low, indicating
low perceptibility and low probability of detection by an observer. Subsequently,
if embedded signal power is much less than the power of an image, an observer
should be unable to visually distinguish the original image from the stegoimage.
To construct the embedded signal the present invention incorporates the concept
of a stored reference spread spectrum communications system {18}. The stored
reference principle requires independent generation of identical pseudorandom
wideband waveforms at both the transmitter and receiver. This can easily
be accomplished by a private or public key {19} and identical pseudorandom
waveform generators. In addition, the pseudorandom number generators can
be cryptographically secure.
First, we describe a simple sign modulation scheme to provide an example
of our spread spectrum process. This method is similar to the technique used
in {20}. Assume that the message signal, m, is a bilevel signal consisting
of {-1,+1} and the spreading sequence, n, is a sequence of real numbers that
have a normal distribution with zero mean and some variance, N. The two signals
are modulated, or multiplied as in Equation (1), resulting in a sequence
of real numbers. In this simple example, the sign of each noise sample is
changed corresponding to the value of the message bit to be embedded. The
white Gaussian characteristics of the signal are preserved. The decoding
process is also elementary. The sequence n is replicated at the receiver,
and the sign of this sequence is compared to the sign of the received embedded
sequence, s, to recover an estimated value of the message signal, m, as shown
in Equation (2).
Although this very simple system meets the necessary requirements of producing
a Gaussian sequence regardless of the message signal values, a major deficiency
lies within the detection of this signal in the presence of noise. This noise
usually results from poor embedded signal estimation but also can be contributed
to by the channel during transmission. Since only the variation of the sign
of embedded signal samples indicates the message, a majority of the values
occur in the vicinity of zero. Moreover, the distance between s when m=-1
and s when m=+1 is typically small, leading to the problematic detection
of m.
Therefore, in order to improve detection performance, a nonlinear modulation
scheme was developed for SSIS. This modulation technique provides an increase
in the minimum Euclidean distance between the possible modulated values,
thereby enabling an improved estimate of the embedded signal over traditional
sign modulation. A flow chart is shown in FIG. 4. This is accomplished by
first generating a uniformly distributed random sequence u with uniform
pseudorandom noise generator 60 using key 2. A second sequence, u', is generated
by applying the piecewise linear transformation of Equation (3) to u with
transformation procedure 62. The embedded signal, s, is then formed by selecting
bits from these two sequences arbitrated by the message bits m, by switch
arbitrator 64 as shown in Equation (4), where .PHI. represents the cumulative
distribution function of a standard Gaussian random variable, Equation (5),
where the inverse of Equation (5) is calculated using the methods presented
in {21}. To adjust the power of the embedded signal a scale factor may be
applied to the embedded signal s in order to further improve detection
performance. This signal is then added to the cover image, the result after
quantization is the stegoimage.
Once obtained at the decoder, the estimate of the embedded signal, s, is
then compared with identical copies of the pseudorandom wideband waveforms,
u and u', used at the encoder to produce an estimate of the hidden message
m. The generation of the identical pseudorandom wideband waveforms is
accomplished by the possession of a common key 2 known only to the sender
and receiver, that is used as a seed for duplicate random number generators.
The method of key encryption may be chosen depending on the level of security
desired.
At the decoder, the stegoimage is obtained and image processing techniques
are used to estimate the embedded signal without knowledge of the original
cover in order to avoid the need for a cover image escrow. By exercising
image restoration techniques at restoration filter 40 an estimate of the
embedded signal can be obtained by subtracting a version of the restored
image f from the stegoimage g, as shown in FIG. 3. Since the pixels of a
digital image are highly correlated among neighboring pixels in natural scenes,
filtering operations can be used to restore the stegoimage so that it resembles
the original image.
The restored image f can be obtained with a variety of image processing filters,
such as mean or median filters, or wavelet shrinkage techniques {22}, and
adaptive Wiener filtering techniques {23}. However, the most favorable
performance, determined by the quality of the recovered embedded signal,
was obtained experimentally with alpha-trimmed mean filtering {27}.
Even though the image restoration yields good performance, the estimate of
such a low power signal necessary to provide the degree of imperceptibility
essential for a steganographic system, is still rather poor. Therefore, in
order to compensate for the suboptimal performance of the signal estimation
process, we have incorporated the use of error control coding. The probability
of error encountered during the estimation process will be referred to as
the embedded signal bit error rate (BER).
The use of error correcting coding by SSIS compensates for the suboptimal
estimation of the embedded signal and combats distortion which may be encountered
during the transmission process. The demodulated message signal may have
a substantial number of bit errors, indicated by a high embedded signal BER.
When a large number of errors are expected to occur in a block of data, an
error-correcting code must be used to correct them. Error correcting codes
within the SSIS system allow the hidden message to be recovered without error
when the transmission channel is noiseless, thus compensating for the noise
estimation process. When the transmission channel is expected to be noisy,
the appropriate low rate error correcting code can be selected to provide
desired performance.
Any error correcting code that has the capability to correct the signal
estimation BER can be used within SSIS. For example, binary expansions of
Reed-Solomon codes {25} were successfully implemented with the SSIS system
of this application. These codes can correct many binary errors if a decoder
is used that corrects bits instead of Reed-Solomon code symbols. The decoders
described in {25} are based on a simple idea of Bossert and Hergert {26}:
if we have a large number of low weight parity checks, then the number of
failing parity checks tends to be proportional to the number of errors. Using
this idea, we can change whichever bits reduce the number of failing parity
checks until no checks fail. This algorithm works very well with binary
expansions of low rate Reed-Solomon codes because they have a large number
of low weight parity checks. With some other improvements described in {25},
these decoders can correct far more binary errors than conventional Reed-Solomon
decoders for the same codes. For example, the (2040,32) decoder corrects
most error patterns with fewer than 763 bit errors, while a conventional
Reed-Solomon decoder would be limited to 125 symbol errors, which is typically
about 165 bit errors. The rate of this (2040,32) code is similar to that
of a (64,1) repetition code, but because it has a much longer block length,
its decoded error rate drops much more quickly as the fraction of errors
per block is reduced.
The SSIS system of the present has been implemented successfully on a standard
UNIX computer. The source code of a preferred implementation is attached
as Appendix A. In general, by increasing the SNR, the performance of embedded
signal estimation is improved at the cost of some imperceptibility.
In order to provide more insight into the presented methodology, a comparison
between the original image pixels of a test image and the stegoimage pixels
is presented in FIG. 5. Here a single row of pixels has been extracted from
both an original 512.times.512 image of an LAV-25 military vehicle containing
256 kilobytes of data and the corresponding stegoimage embedded with high
SNR. In this example the hidden message is a compressed ASCII file containing
the 1783 Treaty of Paris which ended the American Revolutionary War. The
steganographic SNR, the ratio of embedded signal power to cover image power,
for the cover images is -35 dB. The embedded signal BER is 0.25, requiring
the use of a 1/6 convolutional code {28} with soft-decision decoding with
a Viterbi algorithm {29} and the use of side information obtained from the
edges of the stegoimage. This coder can correct a block that is 27% in error.
This yields a payload of 5.4 kilobytes of hidden information. Depending on
the error correction method used, still higher payloads may be obtained.
It is evident from the graph that slight discrepancies between the two exist.
However these discrepancies are undetectable by human observer. Furthermore,
without possession of the original image, the embedded signal is undetectable
by statistical analysis by computer.
Additional protection can be provided for scenarios where additional errors
are expected from the transmission process, such as those encountered in
wireless environments or in lossy image compression, by using lower rate
codes than those dictated by the signal estimation BER.
While the primary thrust of the invention of this application is directed
to embedding of messages in digital images, the methods of the present invention
could be used embed messages in virtually any kind of broadband digital signal
such as high fidelity digital audio. The restoration filter would be designed
to recover the particular information transmitted, such as digital audio.
Other such modifications would be readily apparent to those of skill in the
art.
It will be readily seen by one of ordinary skill in the art that the present
invention fulfills all of the objects set forth above. After reading the
foregoing specification, one of ordinary skill will be able to effect various
changes, substitutions of equivalents and various other aspects of the present
invention as broadly disclosed herein. It is therefore intended that the
protection granted hereon be limited only by the definition contained in
the appended claims and equivalents thereof.
Having thus shown and described what is at present considered to be preferred
embodiments of the present invention, it should be noted that the same have
been made by way of illustration and not limitation. Accordingly, all
modifications, alterations and changes coming within the spirit and scope
of the present invention are herein meant to be included.
REFERENCES
{1} D. Kahn. The Codebreakers--The story of--secret writing. Scribner, New
York, N.Y., 1967.
{2} B. Pfitzmann. Trials of traced traitors. In R. Anderson, editor, Information
Hiding, First International Workshop. Lecture Notes in Computer Science,
pages 49-64. Springer-Verlag, Berlin, 1996.
{3} C. Osborne R. van Schyndel, A. Tirkel. A digital watermark. Proceedings
of the IEEE International Conference on Image Processing, 2:86-90, 1994.
{4} R. Machado. Stego.
http://www.fqa.com/romana/romanasoft/stego.html.
{5} R. B. Wolfgang and E. J. Delp. A watermark for digital images. Proceedings
of the IEEE International Conference on Image Processing, Lausanne, Switzerland,
III:219-222, September 1996.
{6} E. Milbrandt.
http://members.iquest.net/.about.mrmil/stego.html,
October 1997. Steganography Info and Archive.
{7} T. Leighton, I. J. Cox, J. Kilian and T. Shamoon. Secure Spread Spectrum
Watermarking for Images, Audio and Video. Proceedings of the IEEE International
Conference on Image Processing, Lausanne, Switzerland, III:243-246, September
1996.
{8} C. I. Podilchuk and W. Zeng. Digital Image Watermarking Using Visual
Models. In B. E. Rogowitz and T. N. Pappas, editors, Human Vision and Electronic
Imaging 11, volume 3016, pages 100-111. SPIE, February 1997.
{9} B. Zhu, M. D. Swanson and A. H. Tewfik. Transparent Robust Image
Watermarking. Proceedings of the IEEE International Conference on Image
Processing, Lausanne, Switzerland, III:211-214, September 1996.
{10} N. Morimoto, W. Bender, D. Gruhl and A. Lu. Techniques for Data Hiding.
IBM Systems Journal, 35(3 & 4), 1996.
{11} B. Zhu, M. D. Swanson and A. H. Tewfik. Robust Data Hiding for Images.
Proceedings of the IEEE Digital Signal Processing Workshop, Loen, Norway,
pages 37-40, September 1996.
{12} M. D. Swanson and A. H. Tewfik. Data Hiding for Multimedia Personalization,
Interaction, and Protection. IEEE Signal Processing Magazine, 14(4):41-44,
July 1997.
{13} Y. Nakamura K. Tanaka and K. Matsui. Embedding Secret Information into
a Dithered Multi-level Image. Proceedings of the IEEE Military Communications
Conference, Monterey, Calif., pages 216-220, 1990.
{14} E. Adelson. Digital Signal Encoding and Decoding Apparatus. U.S. Pat.
No. 4,939,515, 1990.
{15} G. B. Rhoads. Steganography Method Employing Embedded Calibration Data.
U.S. Pat. No. 5,636,292, 1997.
{16} M. Cooperman. Steganographic Method and Device. U.S. Pat. No. 5,613,004,
1997.
{17} A. K. Jain. Fundamentals of Digital Image Processing. Prentice-Hall,
Inc., Englewood Cliffs, N.J., 1989.
{18} R. A. Scholtz, M. K. Simon, J. K. Omura and B. K. Levitt. Spread Sprectrum
Communications, Volume L Computer Science Press, Rockville, Md., 1985.
{19} B. Schneier. Applied Cryptography--Protocols, Algorithms., and Source
Code in C. John Wiley and Sons, Inc., New York, N.Y., 1996.
{20} F. Hartung and B. Girod. Fast Public Key Watermarking of Compressed
Video. Proceedings of the IEEE International Conference on Image Processing,
Santa Barbara, Calif., October 1997.
{21} M. Abramowitz and I. A. Stegun. Handbook of Mathematical Functions with
Formulas, Graphs, and Mathematical Tables. Dover Publications, Inc., New
York, N.Y., 1964.
{22} D. L. Donoho. De-noising by Soft-thresholding. IEEE Transactions on
Information Theory, 41(3):613-627, 1995.
{23} J. S. Lim. Two-Dimensional Signal and Image Processing. Prentice-Hall,
Inc., Englewood Cliffs, N.J., 1990.
{24} J. S. Lee. Digital Image Enhancement and Noise Filtering by Use of Local
Statistics. IEEE Transactions on Pattern Analysis and Machine Intelligence,
2:165-168, March 1980.
{25} C. T. Retter. Decoding Binary Expansions of Low-rate Reed-Solomon Codes
Far Beyond the BCH Bound. Proceedings of the 1995 IEEE International Symposium
on Information Theory, Whistler, British Columbia, page 276, September 1995.
{26} M. Bossert and F. Hergert. Hard- and Soft-decision Decoding Beyond the
Half Minimum Distance--an Algorithm for Linear Codes. IEEE Transactions on
Information Theory, 32(5):709-714, September 1986.
{27} J. Bee Bednar and Terry L. Watt. Alpha-Trimmed Means and Their Relationship
to Median Filters. IEEE Transactions on Acoustics, Speech and Signal Processing,
Vol. ASSP-32, No. 1, pp. 145-153, February, 1984.
{28} L. J. Harcke and G. E. Wood. Laboratory and Flight Performance of the
Mars Pathfinder (15,1/6) Convolutionally Encoded Telemetry Link. National
Aeronautics and Space Administration (NASA), NASA/JPL TDA Progress Report
42-129, NASA Code 624-04-00-MN-20, May, 1997.
{29} A. J. Viterbi, Error Bounds for Convolutional Codes and an Asymptotically
Optimum Decoding Algorithm, IEEE Transactions on Information Theory, April,
1967, Vol. IT-13, No. 2, pp.260-269.