26 June 1998
Source:
ftp://ftp.rsa.com/pub/pdfs/bulletn7.pdf
(224K)
For current information see: http://www.rsa.com/rsalabs/pkcs1/
NUMBER 7 — JUNE 26, 1998
RSA Laboratories’
News and advice on data security and cryptography
RSA Laboratories®
A Division of RSA Data Security
____________________________________________________
Daniel Bleichenbacher
Bell Laboratories
700 Mountain Ave., Murray Hill, NJ 07974
Burt Kaliski
RSA Laboratories
20 Crosby Drive, Bedford, MA 01730
Jessica Staddon
RSA Laboratories
2955 Campus Drive, Suite 400, San Mateo, CA 94403
Daniel Bleichenbacher is a member of the technical staff at Bell Laboratories; he can be reached at bleichen@research.bell-labs.com. Burt Kaliski is chief scientist and Jessica Staddon is a research scientist at RSA Laboratories; they can be reached at burt@rsa.com and jstaddon@rsa.com, respectively.
This bulletin describes a recently devised attack on PKCS #1 v1.5, the RSA
Encryption Standard [3]. This attack affects only the digital
envelope portion of PKCS #1. In the following sections we describe the digital
enveloping method in PKCS #1 and the new attack. We also describe a variety
of countermeasures that successfully thwart the attack, in particular, we
describe the countermeasure to be found in PKCS #1 v2.
PKCS #1, the first of RSA Laboratories’ Public-Key Cryptography Standards, defines an encoding method for RSA encryption, where a data value D (often a key) is converted to an integer prior to encryption with an RSA public key. Let k be the length in bytes of the recipient’s RSA modulus. The encoding method produces a k-byte string from D of the form
EB = 00 02 || PS || 00 || D
where 00 and 02 are bytes with value 0 and 2, PS is a padding string consisting of k–||D||–3 pseudorandomly generated nonzero bytes, || denotes concatenation, and ||D|| is the length in bytes of the data value D. The second 00 byte separates PS from D.
The sender converts the string EB to an integer m, most significant byte first, and encrypts the result with RSA by the usual exponentiation, c = me mod n where (n,e) is the recipient’s public key, and sends the ciphertext c to the recipient.
The recipient decrypts the ciphertext c with RSA as m = cd mod n, converts the integer m to a string EB, checks that the result has the expected form, and if so, recovers the data value D. The recipient may then check that the data value D has some expected length or form, although this is not required by PKCS #1.
A discussion of the security properties of this encoding method can be found in [7].
The PKCS #1 encoding format for RSA encryption is intended primarily to provide confidentiality, typically for distribution of symmetric encryption keys. It is not intended to provide integrity. In particular, it is not “plaintext-aware”. Informally, an encryption scheme is said to be plaintext-aware if it is infeasible to construct a valid ciphertext without actually knowing the corresponding plaintext. In PKCS #1, whereas it is difficult to recover a data value D from a ciphertext c, it is not difficult to construct a ciphertext c, without knowing the corresponding data value D, that will be decrypted successfully by a recipient. Integrity can be assured by other means than PKCS #1 RSA encryption; however, PKCS #1 does not give any guidance as to what these “other means” might be.
Assuming “other means” for any security service has its pitfalls, and in the case of PKCS #1, leaving those other means to the implementation can introduce a potential vulnerability if integrity is not properly provided.
Suppose that a recipient, after performing the PKCS #1 decryption operation, outputs an error message if it finds that the result does not have the expected form, but otherwise continues processing. An opponent can then determine from the recipient’s behavior some information about the decryption of an arbitrary ciphertext. Indeed, with the PKCS #1 encoding method, the opponent can determine an entire byte and possibly more, when the recipient does not output an error message indicating that the decryption has the wrong form, because the opponent will know that the decryption starts with bytes 00 02. The recipient thus becomes an “oracle” in the theoretical sense for determining particular bits of the decryption of an arbitrary ciphertext.
The ability to predict certain bits of an RSA decryption has previously been shown to provide a means for computing all bits of a decryption [1]. Recently, the first author of this bulletin showed that one can also compute all bits of a decryption from the bits revealed by successful PKCS #1 decryptions of adaptively chosen ciphertexts [3]. Thus the “oracle” just mentioned enables an opponent to compute the decryption of a selected ciphertext with a chosen-ciphertext attack.
The attack has following general form:
1. An opponent has a ciphertext c and wishes to determine its decryption m.
2. The opponent generates a series of related ciphertexts c1 , c2 , ... where
ci = c rie mod n,
r1 , r2 , ... are values between 1 and n–1, and (n,e) is the recipient’s public key. The opponent chooses the values ri in an adaptive way. In particular, the opponent may try to optimize the probability of getting “good” ciphertexts by choosing ri in a way that’s dependent on previous “good” ciphertexts. A ciphertext is “good” if the recipient does not output an error message indicating that the format of corresponding plaintext does not conform with PKCS #1.
3. The opponent submits ciphertexts c1 , c2 , ... to the recipient for decryption in a protocol involving PKCS #1, and observes the recipient’s behavior.
4. From the “good” ciphertexts, the opponent infers certain bits of the corresponding message mi = cid = mri mod n, based on the PKCS #1 encoding method.
5. From the inferred bits of mri mod n for sufficiently many ri values, the opponent is able to reduce the size of the interval that must contain the unknown message m (each “good” ciphertext essentially halves the interval in question). With enough good ciphertexts, then, the opponent is able to determine m.
With the present PKCS #1 encoding method, roughly one in every 216 to 218 randomly chosen ciphertexts will be “good”. This assumes that the bitlength of the public modulus n is as usual a multiple of 8 and that the length of data value D is not checked after decryption. A public modulus n with a bitlength not divisible by 8 would increase this probability, while the probability would be somewhat lower when the recipient also verifies the length of the data block D (in addition to checking only the first two bytes of EB).
Typically, for a 1024-bit modulus, the total number of ciphertexts required is about 220 , and this is also the number of queries to the recipient.
Were the encoding method plaintext-aware, of course, the probability that a ciphertext is “good” would be negligible, thereby defeating the attack.
The practical impact of the attack depends on the protocol of interest. Against an electronic mail encryption protocol, the impact is not significant, since a recipient is unlikely to be willing to process 220 messages, and is unlikely to reveal consistently whether a decryption operation has succeeded or failed. Against an interactive key establishment protocol such as SSL, however, the impact is significant, since a recipient, in this case a server, is willing to process many messages, and may reveal the success or failure of an operation. Moreover, a protocol such as SSL may not require client authentication, so the opponent can easily remain anonymous.
A number of countermeasures are available for the attack just described, most of which are readily implemented.
First we note that good key management practices can be helpful in thwarting this attack (especially when employed with other countermeasures). For example, if a server’s key pair is changed frequently then ciphertexts encrypted using old keys are protected from this attack. In addition, it is a good practice to use different key pairs for different servers, since otherwise an attacker may be able to benefit from using the attack in parallel on many different servers.
Another effective countermeasure relies on the fact that it is often possible to reduce the probability of getting “good” ciphertexts by rigorously checking the format of the message after decryption. In particular if the data block has a fixed length then the length should be checked by the receiver. Other redundancy, such as the version number included in SSL should be checked as well. An identical error message should be sent by the receiver for every possible type of failure in the same amount of time, so that it is not possible to extract information from either the type of error message or by a timing analysis on the receiver’s response time. Checking the length of the data block for a 1024-bit key in SSL would increase the number of chosen messages from approximately 1 million to about 20 million. More than 240 chosen messages might be required for an attack if the version number is also checked. These changes are easy to implement, since they do not change the protocol.
Yet another option is for the recipient to require the sender to demonstrate knowledge of the data value D before the recipient indicates whether a decryption operation is successful. This countermeasure involves no changes to the PKCS #1 encoding method or to the data value D, and requiring such demonstration of knowledge is a prudent measure against other potential attacks.
In its key establishment phase, SSL [5] already requires that the client demonstrate knowledge of the session key that the client has sent to the server in encrypted form. However, some implementations of SSL (e.g., Netscape’s [8]) will return one of two error messages after a failed decryption, and an attacker can obtain useful information by distinguishing between the two errors. A simple patch to such implementations of SSL, therefore, is to consolidate the two error messages into one, as mentioned above; such patches are in the process of being deployed and are available through RSA Data Security’s web page, www.rsa.com, or from the various SSL server vendors.
Almost as simple as any of the previous options is to add structure to the data value D, for instance to concatenate a hash of D to the original data value. The probability that a ciphertext is “good” is thus significantly reduced. This involves changes to the data value D but not to the PKCS #1 encoding method. However, it should be done carefully, so as to avoid introducing too much similarity in the case that the same data value is encrypted on more than one occasion with the same recipient’s public key, which could lead to a vulnerability against an attack due to Coppersmith [4].
Preferable to the previous approaches is a change in the encoding method itself, and this is the approach RSA Laboratories is taking in its current revisions to PKCS #1, which were announced late last year in CryptoBytes. PKCS #1 v2 will support Optimal Asymmetric Encryption Padding (OAEP) [2], which is plaintext-aware and has other desirable security attributes. RSA Laboratories is pursuing similar improvements to public-key standards in IEEE and ANSI. In the interests of interoperability, a single general OAEP encoding method is desirable; the revised PKCS #1, which is intended to be aligned with the IEEE and ANSI X9 standards, will provide a common reference.
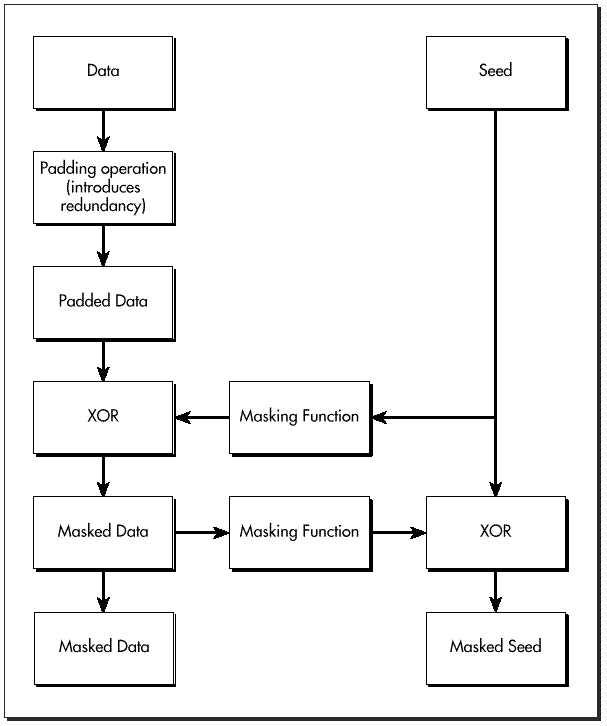
OAEP uses a padding of the data to be encoded and a “mixing” process
to achieve plaintext-awareness. The data is first padded (for specific ways
in which this is done, see [2] and [6])
to give it distinct structure. A masking function, which ideally is a
pseudorandom function, is then applied to a seed and the exclusive-or of
the output from this function and the padded data is taken, creating the
“masked data”. The masked data is then input to another masking
function and the exclusive-or of this output and the seed is taken, creating
the “masked seed”. The concatenation of the masked data and the
masked seed forms the OAEP encoding (see Figure 1, below).

Figure 1. OAEP encoding
To decode the data, the masked data is input to the masking function and the exclusive-or of the output and the masked seed is taken to recover the seed. The seed is then input to the masking function and the exclusive-or of the output and the masked data is taken to recover the padded data. The padding is then checked for the expected structure, and if the structure is present, the data is output.
Because of the random nature of the masking function and the structure of the padding, it is infeasible to create a message that is a valid OAEP encoding of some data string, without knowing the data string beforehand. Therefore if data is OAEP-encoded prior to being encrypted a chosen-ciphertext attack such as the one described above is ineffective: an opponent cannot construct “good” ciphertexts.
Finally, a recipient may keep track of the number of “bad” ciphertexts. A large number may indicate that an attack is in progress, and that the recipient should determine their source.
The PKCS #1 encoding method is not broken, nor is the RSA algorithm, but certain protocols based on PKCS #1 have been shown to be vulnerable to attack.
The practical impact of the attack, which has not yet been carried out on an actual system, remains to be determined. The main impact is on interactive protocols, such as SSL. The relatively large message requirement remains a deterrent, and there are several countermeasures.
1. W. Alexi, B. Chor, O. Goldreich and C. P. Schnorr. RSA and Rabin functions: certain parts are as hard as the whole. SIAM Journal on Computing, 17(2):194-209, April 1988.
2. M. Bellare and P. Rogaway. Optimal asymmetric encryption. In A. de Santis, editor, Advances in Cryptology-Eurocrypt ‘94, pages 92-111, Springer-Verlag, 1995.
3. D. Bleichenbacher. Chosen ciphertext attacks against protocols based on the RSA encryption standard PKCS #1. To appear in Advances in Cryptology-Crypto ‘98.
4. D. Coppersmith. Low-exponent RSA with related messages. In Ueli Maurer, editor, Advances in Cryptology-Eurocrypt ‘96, pages 1-9, Springer-Verlag, 1996.
5. A. O. Freier, P. Karlton, and P. C. Kocher. The SSL Protocol, Version 3.0. Netscape, March 1996.
6. D. B. Johnson and S. M. Matyas. Asymmetric encryption: evolution and enhancements. RSA Laboratories’ CryptoBytes, 2:3, pages 1-6, Spring 1996.
7. B. Kaliski and M. Robshaw. The secure use of RSA. RSA Laboratories’ CryptoBytes, 1:3, pages 7-13, Autumn 1995.
8. SSLRef, a reference implementation from Netscape Communications of the SSL protocol, is available at http://home.netscape.com/newsref/std/sslref.html.
Developers are encouraged to adopt the new encoding method forthcoming
in PKCS #1 v2, and to consider some of the other countermeasures mentioned
above. For more information on the new result and on the revisions to PKCS
#1, readers are welcome to contact RSA Laboratories at the address below.
RSA Laboratories |
Copyright © 1998 RSA Laboratories, a division of RSA Data Security, Inc., a Security Dynamics Company. All rights reserved.