5 June 2005
Source:
http://patft.uspto.gov/netacgi/nph-Parser?Sect1=PTO1&Sect2=HITOFF&d=PALL&p=1&u=/netahtml/srchnum.htm&r=1&f=G&l=50&s1=6,898,284.WKU.&OS=PN/6,898,284&RS=PN/6,898,284
| United States Patent |
6,898,284 |
| Solinas |
May 24, 2005 |
Cryptographic identification and digital signature method
using efficient elliptic curve
Abstract
A method of identifying user, generating digital signature, and verifying
digital signature by selecting a modulus p in the form of
p=(2dk-2ck-1)/r,
p=(2dk-2(d-1)k+2(d-2)k- . . .
-2k+1)/r, p=(2dk-2ck-1)/r,
p=(2dk-2ck+1)/r, and
p=(24k-23k+22k+1)/r, selecting an elliptic
curve E and an order q; selecting a basepoint G; generating a private key
w; generating a public key W=wG; distributing p, E, q, G, and W to at least
a prover, a verifier, and a signer; generating the prover's private key
wp and public key Wp=wpG; retrieving the
prover's public key Wp; generating a private integer
kp; combining kp and G to form K using p; sending K
to the verifier; sending a challenge integer c to the prover; combining c,
kp, and wp to form a response integer v; sending v
to the verifier; combining cG, K, and Wp using p and checking
to see if the combination is equal to vG. If not so, stop. Otherwise, generating,
by the signer, the signer's private key ws; generating a private
integer ks; combining ks and G to form K using p; combining
K and a message M to form an integer h; combining h, ks, and ws
to form an integer s; sending M and (K,s) as a digital signature of
M; retrieving Wp; receiving M and (K,s); combining K and M to
form an integer h; and combining h, K, and Wp using p and checking
to see if the combination is equal to sG. If so, the digital signature is
verified.
| Inventors: |
Solinas; Jerome Anthony (Westminster,
MD) |
| Assignee: |
The United States of America as represented
by the National Security Agency (Washington, DC) |
| Appl. No.: |
928266 |
| Filed: |
August 9, 2001 |
| Current U.S. Class: |
380/28; 380/30; 713/161;
713/171; 713/174 |
| Intern'l Class: |
H04L 009//06; H04L 009//30 |
| Field of Search: |
235/451 380/1,28,30,231,265,285
708/491,492,523,620 713/161,171,174,189,193,194,500 |
References Cited
[Referenced
By]
U.S. Patent Documents
Other References
D. Johnson and A. Menezes, "The Elliptic Curve Digital Signature Algorithm
(ECDSA)," University of Waterloo, Aug. 23, 1999, http://cacr.math.waterloo.ca.*
J. Solinas. "Generalized mersenne numbers". Technical Report CORR-39, University
of Waterloo, Sep. 1999, also available at http://cacr.math.waterloo.ca.*
FIPS PUB 186-2, Jan. 27, 2000, Digital Signature Standard, U.S. Dept. of
Commerce (NIST).
Victor S. Miller, "Use of Elliptic Curves in Cryptography", Advances in
Cryptography-Crypto 85, LNCS 218, pp. 417-426, 1986.
Neil Kobutz, "A Course in Number Theory and Cryptography," QA 241.K672, 1987,
pp. 150-179.
Peter L. Montgomery, "Modular Multiplication Without Trail Division," Mathematics
of Computation, vol. 44, No. 170, Apr. 1985 pp. 519-521. |
Primary Examiner: Caldwell; Andrew
Assistant Examiner: Teslovich; Tamara
Attorney, Agent or Firm: Morelli; Robert D.
Parent Case Text
This application claims the benefit of U.S. Provisional Application No.
60/226,209, filed Aug. 18, 2000.
Claims
1. A method of identifying a user, comprising the steps of:
a) selecting, by the user, a modulus p from the group of equations consisting
of:
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1;
where d is even, and where k is not equal to 2 (mod 4);
where 3d<6c<4d, and where GCD(c,d)=1;
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1; and
b) selecting, by the user, an elliptic curve E and an order q;
c) selecting, by the user, a basepoint G;
d) generating, by the user, a private key w;
e) generating, by the user, a public key W=wG;
f) distributing, by the user, p, E, q, G, and W in an authentic manner;
g) generating, by a prover, the prover's private key wp and public
key Wp and distributing Wp;
h) retrieving, by a verifier, the prover's public key Wp;
i) generating, by the prover, a private integer kp;
j) combining, by the prover, kp and G to form K using the form
of the modulus p;
k) sending, by the prover, K to the verifier;
l) sending, by the verifier, a challenge integer c to prover;
m) combining, by the prover, c, kp, and wp to form
a response integer v;
n) sending, by the prover, v to the verifier; and
o) combining, by the verifier, cG, K, and Wp using the form of
the modulus p and checking to see if the combination is equal to vG, if so
the user is identified as the user, otherwise the user is not identified
as the user.
2. The method of claim 1, further comprising the steps of:
a) generating, by a signer, the signer's private key ws;
b) generating, by the signer, a private integer ks;
c) combining, by the signer, ks and G to form K using the form
of the modulus p;
d) combining, by the signer, K and a message M to form an integer h;
e) combining by the signer, h, ks, and ws to form an
integer s; and
f) sending, by the signer, M and (K,s) as a digital signature of M.
3. The method of claim 2, further including the steps of:
a) retrieving, by the verifier, the prover's public key Wp;
b) receiving, by the verifier, M and (K,s);
c) combining, by the verifier, K and M to form an integer h; and
d) combining, by the verifier, h, K, and Wp using the form of
the modulus p and checking to see if the combination is equal to sG, if so
then the digital signature is verified, otherwise the digital signature is
not verified.
4. The method of claim 1, further comprising the steps of:
a) generating, by a signer, the signer's private key ws;
b) generating, by the signer, a private integer ks;
c) combining, by the signer, ks and G to form K using the form
of the modulus p;
d) combining, by the signer, K and a message M to form an integer h;
e) combining by the signer, h, ks, and ws to form an
integer s; and
f) sending, by the signer, M and (h,s) as a digital signature of M.
5. The method of claim 4, further including the steps of:
a) retrieving, by the verifier, the prover's public key Wp;
b) receiving, by the verifier, M and (h,s);
c) combining, by the verifier, h, Wp, and sG using the form of
the modulus p to form K;
d) combining, by the verifier, K and M to form an integer h2; and
e) checking, by the verifier, that h is equal to h2, if so then the digital
signature is verified, otherwise the digital signature is not verified.
Description
FIELD OF THE INVENTION
The present invention relates, in general, to cryptography and, in particular,
to public key cryptography.
BACKGROUND OF THE INVENTION
Cryptography provides methods of providing privacy and authenticity for remote
communications and data storage. Privacy is achieved by encryption of data,
usually using the techniques of symmetric cryptography (so called because
the same mathematical key is used to encrypt and decrypt the data). Authenticity
is achieved by the functions of user identification, data integrity, and
message non-repudiation. These are best achieved via asymmetric (or public-key)
cryptography.
In particular, public-key cryptography enables encrypted communication between
users that have not previously established a shared secret key between them.
This is most often done using a combination of symmetric and asymmetric
cryptography: public-key techniques are used to establish user identity and
a common symmetric key, and a symmetric encryption algorithm is used for
the encryption and decryption of the actual messages. The former operation
is called key agreement. Prior establishment is necessary in symmetric
cryptography, which uses algorithms for which the same key is used to encrypt
and decrypt a message. Public-key cryptography, in contrast, is based on
key pairs. A key pair consists of a private key and a public key. As the
names imply, the private key is kept private by its owner, while the public
key is made public (and typically associated to its owner in an authenticated
manner). In asymmetric encryption, the encryption step is performed using
the public key, and decryption using the private key. Thus the encrypted
message can be sent along an insecure channel with the assurance that only
the intended recipient can decrypt it.
The key agreement can be interactive (e.g., for encrypting a telephone
conversation) or non-interactive (e.g., for electronic mail).
User identification is most easily achieved using what are called identification
protocols. A related technique, that of digital signatures, provides data
integrity and message non-repudiation in addition to user identification.
The use of cryptographic key pairs was disclosed in U.S. Pat. No. 4,200,770,
entitled "CRYPTOGRAPHIC APPARATUS AND METHOD." U.S. Pat. No. 4,200,770 also
disclosed the application of key pairs to the problem of key agreement over
an insecure communication channel. The algorithms specified in this U.S.
Pat. No. 4,200,770 rely for their security on the difficulty of the mathematical
problem of finding a discrete logarithm. U.S. Pat. No. 4,200,770 is hereby
incorporated by reference into the specification of the present invention.
In order to undermine the security of a discrete-logarithm based cryptoalgorithm,
an adversary must be able to perform the inverse of modular exponentiation
(i.e., a discrete logarithm). There are mathematical methods for finding
a discrete logarithm (e.g., the Number Field Sieve), but these algorithms
cannot be done in any reasonable time using sophisticated computers if certain
conditions are met in the specification of the cryptoalgorithm.
In particular, it is necessary that the numbers involved be large enough.
The larger the numbers used, the more time and computing power is required
to find the discrete logarithm and break the cryptography. On the other hand,
very large numbers lead to very long public keys and transmissions of
cryptographic data. The use of very large numbers also requires large amounts
of time and computational power in order to perform the cryptoalgorithm.
Thus, cryptographers are always looking for ways to minimize the size of
the numbers involved, and the time and power required, in performing the
authentication algorithms. The payoff for finding such a method is that
cryptography can be done faster, cheaper, and in devices that do not have
large amounts of computational power (e.g., hand-held smart-cards).
A discrete-logarithm based cryptoalgorithm can be performed in any mathematical
setting in which certain algebraic rules hold true. In mathematical language,
the setting must be a finite cyclic group. The choice of the group is critical
in a cryptographic system. The discrete logarithm problem may be more difficult
in one group than in another for which the numbers are of comparable size.
The more difficult the discrete logarithm problem, the smaller the numbers
that are required to implement the cryptoalgorithm. Working with smaller
numbers is easier and faster than working with larger numbers. Using small
numbers allows the cryptographic system to be higher performing (i.e., faster)
and requires less storage. So, by choosing the right kind of group, a user
may be able to work with smaller numbers, make a faster cryptographic system,
and get the same, or better, cryptographic strength than from another
cryptographic system that uses larger numbers.
The groups which were envisioned in the above-named patents come from a setting
called finite fields. A book by N. Koblitz, "A Course in Number Theory and
Cryptography," (1987), and a paper by V. Miller, "Use of elliptic curves
in cryptography," Advances in Cryptology—CRYPTO 85, LNCS 218, pp. 417-426,
1986, disclose the method of adapting discrete-logarithm based algorithms
to the setting of elliptic curves. It appears that finding discrete logarithms
in this kind of group is particularly difficult. Thus elliptic curve-based
cryptoalgorithms can be implemented using much smaller numbers than in a
finite-field setting of comparable cryptographic strength. Thus the use of
elliptic curve cryptography is an improvement over finite-field based public-key
cryptography.
There are several kinds of elliptic curve settings. These settings have
comparable cryptographic strength and use numbers of comparable size. However,
these settings differ in the amount of computation time required when
implementing a cryptoalgorithm. Cryptographers seek the fastest kind of elliptic
curve based cryptoalgorithms.
More precisely, an elliptic curve is defined over a field F. An elliptic
curve is the set of all ordered pairs (x,y) that satisfy a particular cubic
equation over a field F, where x and y are each members of the field F. Each
ordered pair is called a point on the elliptic curve. In addition to these
points, there is another point O called the point at infinity. The infinity
point is the additive identity (i.e., the infinity point plus any other point
results in that other point). For cryptographic purposes, elliptic curves
are typically chosen with F as the integers mod p for some large prime number
p (i.e., Fp) or as the field of 2^m elements.
To carry out an elliptic curve-based key agreement procedure, it is necessary
to perform a sequence of operations involving points on the curve and the
equation of the curve. Each of these operations is carried out via arithmetic
operations in the field F, namely addition, subtraction, multiplication,
and division. If F is the set of integers mod p, then the simplest and most
common way to carry out the arithmetic operations is to use ordinary integer
arithmetic along with the process of reduction modulo p. This last process
is called modular reduction.
Modular reduction is the most expensive part of the arithmetic operations
in the field Fp. Therefore, the efficiency of an elliptic curve algorithm
is enhanced when the cost of modular reduction is reduced. There are two
common ways of doing this.
The first way is to avoid explicit modular reduction altogether by using
an alternative method of carrying out the arithmetic operations in the field
Fp. This was first proposed by P. Montgomery in the paper "Modular multiplication
without trial division," Mathematics of Computation, 44 (1985), pp. 519-521.
This method has the advantage that it can be applied to both elliptic and
non-elliptic cryptoalgorithms.
The second way is to choose the prime modulus p in such a way that modular
reduction is particularly easy and efficient. This approach yields faster
elliptic curve algorithms than the first approach, but does not apply to
non-elliptic cryptoalgorithms.
More specifically, suppose that one needs to reduce an integer b modulo p.
Typically, b is a positive integer less than the square of the modulus p.
In the general case, the best way to reduce b modulo p is to divide b by
p; the result is a quotient and a remainder. The remainder is the desired
quantity. The division step is the most expensive part of this process. Thus
the prime modulus p is chosen to avoid the necessity of carrying out the
division.
The simplest and best-known choice is to let p be one less than a power of
two. Such primes are commonly called Mersenne primes. Because of the special
form of a Mersenne prime p, it is possible to replace the division step of
the modular reduction process by a single modular addition. A modular addition
can be carried out using one or two integer additions, and so is much faster
than an integer division. As a result, reduction modulo a Mersenne prime
is much faster than in the general case.
A larger class of primes which contains the Mersenne primes as a special
case is the class of pseudo-Mersenne primes. These include the Crandall primes
and the Gallot primes. The Crandall primes are those of the form 2^m±C,
where C is an integer less than 2^32 in absolute value. The Gallot primes
are of the form k*2^m±C, where both k and C are relatively small.
U.S. Pat. No. 5,159,632, entitled "METHOD AND APPARATUS FOR PUBLIC KEY EXCHANGE
IN A CRYPTOGRAPHIC SYSTEM"; U.S. Pat. No. 5,271,061, entitled "METHOD AND
APPARATUS FOR PUBLIC KEY EXCHANGE IN A CRYPTOGRAPHIC SYSTEM"; U.S. Pat. No.
5,463,690, entitled "METHOD AND APPARATUS FOR PUBLIC KEY EXCHANGE IN A
CRYPTOGRAPHIC SYSTEM"; U.S. Pat. No. 5,581,616, entitled "METHOD AND APPARATUS
FOR DIGITAL SIGNATURE AUTHENTICATION"; U.S. Pat. No. 5,805,703, entitled
"METHOD AND APPARATUS FOR DIGITAL SIGNATURE AUTHENTICATION"; and U.S. Pat.
No. 6,049,610, entitled "METHOD AND APPARATUS FOR DIGITAL SIGNATURE
AUTHENTICATION"; each disclose the use of a class of numbers in the form
of 2^q-C which make modular reduction more efficient and therefore, make
cryptographic methods such as key exchange and digital signatures more efficient.
The present invention does not use a class of numbers in the form of 2^q-C.
U.S. Pat. Nos. 5,159,632; 5,271,061; 5,463,690; 5,581,616; 5,805,703; and
6,049,610 are hereby incorporated by reference into the specification of
the present invention.
Federal Information Processing Standards Publication 186-2 (i.e., FIPS PUB
186-2) discloses a digital signature standard. In the appendix of FIPS PUB
186-2 are recommended elliptic curves for a 192-bit, a 224-bit, a 256-bit,
a 384-bit, and a 521-bit digital signature. The elliptic curves disclosed
in FIPS PUB 186-2 are different from the elliptic curves used in the present
invention.
SUMMARY OF THE INVENTION
It is an object of the present invention to efficiently create a digital
signature using a modulus p selected from the following families of equations:
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1, where
GCD is a function that returns the greatest common denominator between the
variables in parenthesis;
where d is even, and where k is not equal to 2 (mod 4);
where 3d<6c<4d, and where GCD(c,d)=1;
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1; and
The first step through sixth step are done by each user who wishes to have
its message digitally signed. The first step is selecting a modulus p from
the following family of equations:
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1;
where d is even, and where k is not equal to 2 (mod 4);
where 3d<6c<4d, and where GCD(c,d)=1;
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1; and
The second step is selecting an elliptic curve E and an order q.
The third step is selecting a basepoint G.
The fourth step is generating a private key w.
The fifth step is generating a public key W=wG.
The sixth step is distributing p, E, q, G, and W in an authentic manner.
The seventh step through fifteenth step are done to identity the user who
wishes to have a message digitally signed. The seventh step is a prover
generating its private key wp and public key
Wp=wpG, and distributing its Wp.
The eighth step is a verifier retrieving the prover's public key
Wp.
The ninth step is the prover generating a private integer kp.
The tenth step is the prover combining kp and G to form K using
the form of the modulus p.
The eleventh step is the prover sending K to the verifier.
The twelfth step is the verifier sending a challenge integer c to prover.
The thirteenth step is the prover combining c, kp, and
wp to form a response integer v.
The fourteenth step is the prover sending v to the verifier.
The fifteenth step is the verifier combining cG, K, and Wp using
the form of the modulus p and checking to see if the combination is equal
to vG. If the combination is equal to vG then the prover is properly identified.
Otherwise, the prover is not properly identified.
The sixteenth step through the twenty-first step are done by the person digitally
signing a message. The sixteenth step is a signer generating its private
key ws.
The seventeenth step is the signer generating a private integer
ks.
The eighteenth step is the signer combining ks and G to form K
using the form of the modulus p.
The nineteenth step is the signer combining K and a message M to form an
integer h.
The twentieth step is the signer combining h, ks, and
ws to form an integer s.
The twenty-first step is the signer sending the message M and the digital
signature (K,s) of M.
The twenty-second step through the twenty-fifth step are done by the person
verifying the digital signature. The twenty-second step is the verifier
retrieving the prover's public key Wp.
The twenty-third step is the verifier receiving M and (K,s).
The twenty-fourth step is the verifier combining K and M to form an integer
h.
The twenty-fifth step is the verifier combining h, K, and Wp using
the form of the modulus p and checking to see if the combination is equal
to sG. If so, then the digital signature is verified. Otherwise, the digital
signature is not verified.
The twenty-sixth step through the thirty-first step are alternative steps
for digitally signing a message. The twenty-sixth step is a signer retrieving
its private key ws.
The twenty-seventh step is the signer generating a private integer
ks.
The twenty-eighth step is the signer combining ks and G to form
K using the form of the modulus p.
The twenty-ninth step is the signer combining K and a message M to form an
integer h.
The thirtieth step is the signer combining h, ks, and
ws to form an integer s.
The thirty-first step through thirty-sixth steps are alternative steps for
verifying the digital signature of the alternative signing steps. The
thirty-first step is the signer sending the message M and the digital signature
(h,s) of M.
The thirty-second step is the verifier retrieving the prover's public key
Wp.
The thirty-third step is the verifier receiving M and (h,s).
The thirty-fourth step is the verifier combining h, Wp, and sG
using the form of the modulus p to form K.
The thirty-fifth step is the verifier combining K and M to form an integer
h2.
The thirty-sixth step is the verifier checking to see if h is equal to h2.
If so, then the digital signature is verified. Otherwise, the digital signature
is not verified.
BRIEF DESCRIPTION OF THE DRAWINGS
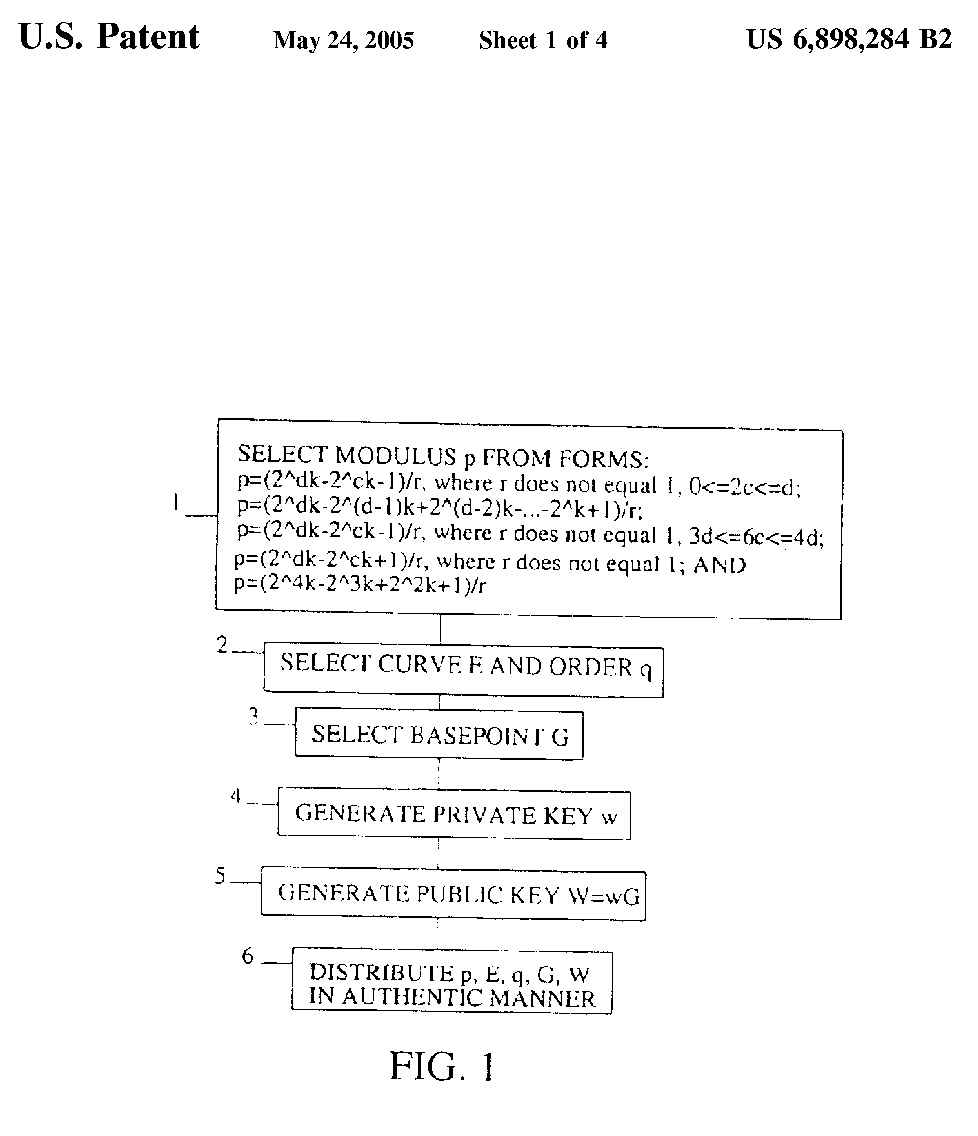
FIG. 1 is a list of steps that must be done by each user;
FIG. 2 is a list of steps for identifying a user;
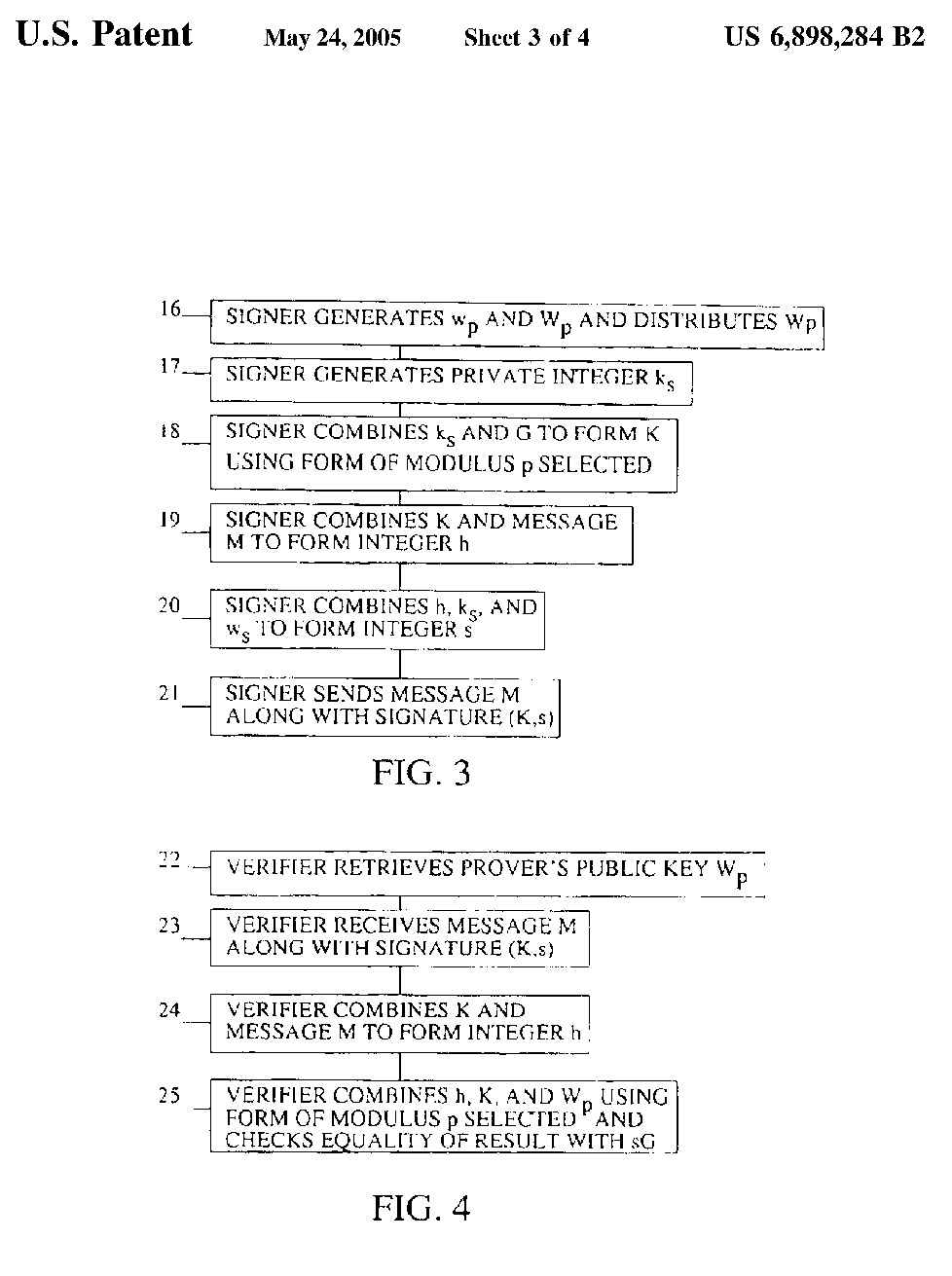
FIG. 3 is a list of steps for signing a digital signature;
FIG. 4 is a list of steps for verifying a digital signature of FIG. 3;
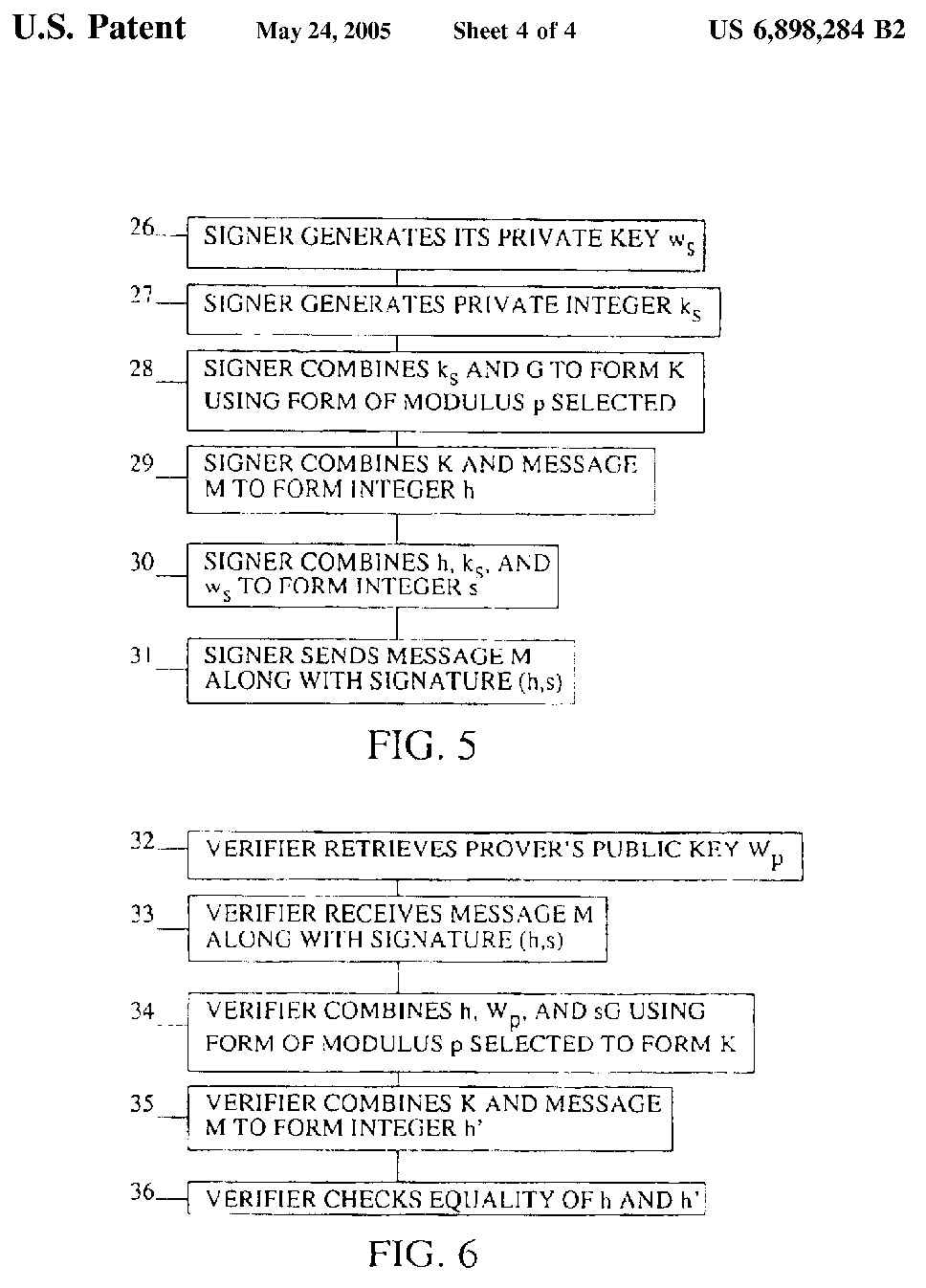
FIG. 5 is a list of alternate steps for signing a digital signature; and
FIG. 6 is a list of alternate steps for verifying a digital signature of
FIG. 5.
DETAILED DESCRIPTION
The present invention is a method of identifying a user, generating a digital
signature for a message of the user, and verifying the digital signature
in an efficient manner (i.e., in fewer steps than the prior art) using a
modulus p selected from the following family of equations:
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1;
where d is even, and where k is not equal to 2 (mod 4);
where 3d<6c<4d, and where GCD(c,d)=1;
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1; and
It has long been known that certain integers are particularly well suited
for modular reduction. The best known examples are the Mersenne numbers
p=2k-1. In this case, the integers (mod p) are represented as
k-bit integers. When performing modular multiplication, one carries out an
integer multiplication followed by a modular reduction. One thus has the
problem of reducing modulo p a 2k-bit number. Modular reduction is usually
done by integer division, but this is unnecessary in the Mersenne case. Let
n<p2 be the integer to be reduced (mod p). Let T be the integer
represented by the k most significant bits of n, and U the k least significant
bits; thus
n=2kT+U,
with T and U each being k-bit integers. Then
Thus, the integer division by m can be replaced by an addition (mod p), which
is much faster.
The main limitation on this scheme is the special multiplicative structure
of Mersenne numbers. The above technique is useful only when one intends
to perform modular arithmetic with a fixed long-term modulus. For most
applications of this kind, the modulus needs to have a specific multiplicative
structure, most commonly a prime number. The above scheme proves most useful
when k is a multiple of the word size of the machine. Since this word size
is typically a power of 2, one must choose k which is highly composite.
Unfortunately, the Mersenne numbers arising from such k are never prime numbers.
It is, therefore, of interest to find other families of numbers that contain
prime numbers or almost prime numbers.
One such family is 2k-c, for c positive, which is disclosed in
U.S. Pat. Nos. 5,159,632; 5,271,061; 5,463,690; 5,581,616; 5,805,703; and
6,049,610 listed above. The present invention discloses the use of other
families of numbers.
FIG. 1 is a list of steps that must be done by each user of the present
invention.
The first step 1 of the present method is selecting a modulus p from the
following family of equations:
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1;
where d is even, and where k is not equal to 2 (mod 4);
where 3d<6c<4d, and where GCD(c,d)=1;
where 0<2c<=d, where r does not equal to 1, and where GCD(c,d)=1; and
The second step 2 of the present method is selecting an elliptic curve E
and an order q.
The third step 3 of the present method is selecting a basepoint G.
The fourth step 4 of the present method is generating a private key w.
The fifth step 5 of the present method is generating a public key W=wG.
The sixth step 6 of the present method is distributing p, E, q, G, and W
in an authentic manner (e.g., courier, secure channel, etc.).
FIG. 2 lists the steps for identifying a user.
 |
|
The seventh step 7 of the method is a prover generating its private key
wp and public key Wp=wpG and distributing
Wp.
The eighth step 8 of the present method is a verifier retrieving the prover's
public key Wp.
The ninth step 9 of the present method is the prover generating a private
integer kp.
The tenth step 10 of the present method is the prover combining kp
and prover's G to form K using the form of the modulus p.
The eleventh step 11 of the present method is the prover sending K to the
verifier.
The twelfth step 12 of the present method is the verifier sending a challenge
integer c to the prover.
The thirteenth step 13 of the present method is the prover combining c,
kp, and wp to form a response integer v.
The fourteenth step 14 of the present method is the prover sending v to the
verifier.
The fifteenth step 15 of the present method is the verifier combining cG,
K, and Wp using the form of the modulus p and checking to see
if the combination is equal to vG. If the combination is equal to vG then
the prover is properly identified. Otherwise, the prover is not properly
identified.
FIG. 3 is a list of steps for signing a digital signature.
 |
|
The sixteenth step 16 of the present method is a signer retrieving its private
key ws.
The seventeenth step 17 of the present method is the signer generating a
private integer ks.
The eighteenth step 18 of the present method is the signer combining
ks and G to form K using the form of the modulus p.
The nineteenth step 19 of the present method is the signer combining K and
a message M to form an integer h.
The twentieth step 20 of the present method is the signer combining h,
ks, and ws to form an integer s.
The twenty-first step 21 of the present method is the signer sending the
message M and the digital signature (K,s) of M.
FIG. 4 is a list of steps for verifying the digital signature generated by
the steps of FIG. 3.
The twenty-second step 22 of the present method is the verifier retrieving
the prover's public key Wp.
The twenty-third step 23 of the present method is the verifier receiving
M and (K,s).
The twenty-fourth step 24 of the present method is the verifier combining
K and M to form an integer h.
The twenty-fifth step 25 of the present method is the verifier combining
h, K, and Wp using the form of the modulus p and checking to see
if the combination is equal to sG. If so, then the digital signature is verified.
Otherwise, the digital signature is not verified.
FIG. 5 is a list of alternate steps for signing a digital signature.
 |
|
The twenty-sixth step 26 of the present method is a signer retrieving its
private key ws.
The twenty-seventh step 27 of the present method is the signer generating
a private integer ks.
The twenty-eighth step 28 of the present method is the signer combining
ks and G to form K using the form of the modulus p.
The twenty-ninth step 29 of the present method is the signer combining K
and a message M to form an integer h.
The thirtieth step 30 of the present method is the signer combining h,
ks, and ws to form an integer s.
The thirty-first step 31 of the present method is the signer sending the
message M and the digital signature (h,s) of M.
FIG. 6 is a list of alternate steps for verifying the digital signature generated
by the steps of FIG. 5.
The thirty-second step 32 of the present method is the verifier retrieving
the prover's public key Wp.
The thirty-third step 33 of the present method is the verifier receiving
M and (h,s).
The thirty-fourth step 34 of the present method is the verifier combining
h, Wp, and sG using the form of the modulus p to form K.
The thirty-fifth step 35 of the present method is the verifier combining
K and M to form an integer h2.
The thirty-sixth step 36 of the present method is the verifier checking to
see if h is equal to h2. If so, then the digital signature is verified.
Otherwise, the digital signature is not verified.
* * * * *