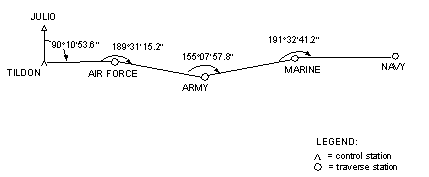
Figure 6-1. Open Traverse
Field Manual 3-34.331 TOPOGRAPHIC SURVEYING 16 January 2001
TOC Chap1 2 3 4 5 6 7 8 9 10 11 AppA AppB AppC AppD Gl Bib
Chapter 6
Traversing is a form of a control survey that is used in a wide variety of surveys. Traverses are a series of established stations that are linked together by the angle and distance between adjacent points. The angles are measured by theodolites, and the distances are measured by an EDME. The AISI total station combines both of these functions. Detailed information pertaining to traverse design, data collection, and limitations are discussed in the SSGCN. Appendix B summarizes the standards for control surveys. Appendix C details the recommended procedures for traverse computations.
6-1. The purpose of a traverse is to locate points relative to each other on a common grid. Surveyors need certain elements of starting data, such as the coordinates of a starting point and an azimuth to an azimuth mark. There are several ways to obtain the starting data, and surveyors should make an effort to use the best data available to begin a traverse. Survey-control data is available in the form of existing stations (with the station data published in a trig list) or new stations (established by local agencies who can provide the station data).
6-2. An open traverse (Figure 6-1) originates at a starting station, proceeds to its destination, and ends at a station with an unknown relative position. The open traverse is the least desirable traverse type, because it does not provide the opportunity for checking the accuracy of the fieldwork. All measurements must be carefully collected, and every procedure for checking position and direction must be used. Therefore, the planning of a traverse should always provide for closure of the traverse.
 |
6-3. A closed traverse either begins and ends on the same point or begins and ends at points with previously determined (and verified) coordinates. In both cases, the angles can be closed and closure accuracy can be mathematically determined.
TRAVERSE CLOSED ON A STARTING POINT6-4. A traverse that starts at a given point, proceeds to its destination, and returns to the starting point without crossing itself in the process is referred to as a loop traverse (Figure 6-2). Surveyors use this type of traverse to provide control if there is little existing control in the area and only the relative position of the points is required. While the loop traverse provides some check of the fieldwork and computations, it does not ensure the detection of all the systematic errors that may occur in a survey.
 |
TRAVERSE CLOSED ON A SECOND KNOWN POINT
6-5. A traverse that is closed on a second known point begins at a point of known coordinates, moves through the required point(s), and terminates at a second point of known coordinates. Surveyors prefer this type of traverse because it provides a check on the fieldwork, computations, and starting data. It also provides a basis for comparing data to determine the overall accuracy of the work.
6-6. In a traverse, three stations are considered to be of immediate significance. These stations are the rear, the occupied, and the forward. The rear station is the station that the surveyors who are performing the traverse have just moved from, or it is a point to which the azimuth is known. The occupied station is the station at which the party is located and over which the instrument is set. The forward station is the immediate destination of the party or the next station in succession.
HORIZONTAL ANGLES6-7. Always measure horizontal angles at the occupied station by sighting the instrument at the rear station and measuring the clockwise angles to the forward station. Make instrument observations to the clearest and most defined and repeatable point of the target that marks the rear and forward stations. Measurements are repeated according to the required specifications.
DISTANCE6-8. Use an EDME to measure the distance in a straight line between the occupied and the forward stations. Measurements are repeated according to the required specifications.
6-9. Select sites for traverse stations as the traverse progresses. Locate the stations in such a way that at any one station both the rear and forward stations are visible. The number of stations in a traverse should be kept to a minimum to reduce the accumulation of instrument errors and the amount of computing required. Short traverse legs (sections) require the establishment and use of a greater number of stations and may cause excessive errors in the azimuth. Small errors in centering the instrument, in station-marking equipment, and in instrument pointings are magnified and absorbed in the azimuth closure as errors in angle measurement.
STATION MARKERS6-10. Station markers are usually 2- by 2-inch wooden stakes, 6 inches or more in length. These stakes (hubs) are driven flush with the ground. The center of the top of the hub is marked with a surveyor's tack or an X to designate the exact point of reference for angular and linear measurements.
6-11. To assist in recovering a station, surveyors drive a reference (witness) stake into the ground so that it slopes toward the station. Surveyors must write the identification of the station on the reference stake or on a tag that is attached to the stake with a lumber crayon or a china-marking pencil. Signal cloth may also be tied to the reference stake to further assist in identifying or recovering a station.
STATION SIGNALS6-12. A signal must be erected over survey stations to provide a sighting point for the instrument operator. The survey target set (discussed in Chapter 5) is the most commonly used signal.
6-13. The number of personnel available to perform survey operations depends on the unit's TOE. The organization of these people into a traverse party and the duties assigned to each member will depend on the unit's SOP. The organization and duties of a traverse party are based on the functional requirements of the traverse.
6-14. The party chief selects and marks the traverse-station locations and supervises the work of the other party members. The party chief also assists in the survey recon and planning.
6-15. The survey team consists of the following members:
- Instrument operator. The instrument operator measures the horizontal angles and distances at each traverse station.
- Recorder. The recorder keeps the field notes in a field notebook and records the angles and distances measured by the instrument operator and all other information pertaining to the survey.
- Rodman. The rodman assists the party chief in marking the traverse stations, removes the target from the rear station when signaled by the instrument operator, and moves the target forward to the next traverse station.
6-16. The azimuth of a line is the horizontal angle (measured clockwise) from a base direction to the line in question. To compute a traverse, surveyors determine the azimuth for each traverse leg. The azimuth for each succeeding leg is determined by adding the value of the measured angle at the occupied station to the value of the azimuth from the occupied station to the rear station. On occupation of each successive station, the first step is to compute the back azimuth of the preceding leg (the azimuth from the occupied station to the rear station).
AZIMUTH ADJUSTMENT6-17. Determine the need for an adjustment before beginning final-coordinate computations. If the angular error of closure (AEC) falls within the computed AE, the azimuths of the traverse may be adjusted. The allowable AEC is determined for third-order, Class I traverse by the following formula:
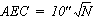
where
10" = AE for a single station
N = the number of traverse segments
If the azimuth error does not fall within the AEC, reobserve the station angles of the traverse in the field.
AZIMUTH CORRECTION6-18. Before determining a correction, compute the actual azimuth error. The azimuth error is obtained by subtracting the known closing azimuth from the computed closing azimuth. This difference provides the angular error with the appropriate sign. By reversing this sign, the azimuth correction (with the appropriate sign) is obtained. If the azimuth correction falls within allowable limits, compute the error and the correction.
6-19. A traverse adjustment is based on the assumption that errors have accumulated gradually and systematically throughout the traverse. An azimuth correction is applied accordingly. The correction is distributed systematically among the angles of the traverse.
6-20. After the angles are adjusted, compute the adjusted azimuth of each leg by using the starting azimuth and the adjusted angles at each traverse station. Compute the adjusted azimuth throughout the entire traverse and check against the correct azimuth to the closing azimuth mark before beginning any further traverse computations.
6-21. The trigonometric functions (such as sine [denoted by sin], cosine [denoted by cos], and tangent [denoted by tan]) of the azimuth and the bearing are numerically the same. Surveyors may use either the azimuth or the bearing to compute the traverse. The choice will depend on the computer and the equipment available.
AZIMUTH AND BEARING6-22. If a calculator with angular functions is available, the use of the azimuth is easier since it eliminates the need to compute the bearing. If the functions must be determined from tables, it is necessary to first compute the bearing angles since the tabulation of functions is normally published for angles of 0� to 90�. The bearing of a line is the acute angle (an angle less than 90�) formed by the line in question and the north-south line through the occupied point. The bearing illustrates the relationship between the azimuth of a line and its direction.
QUADRANTS6-23. Bearing angles are computed from a given azimuth depending on the quadrant in which the azimuth lies. When the azimuth is in the first quadrant (0� to 90�), the bearing is equal to the azimuth. When the azimuth is in the second quadrant (90� to 180�), the bearing is equal to 180� minus the azimuth. When the azimuth is in the third quadrant (180� to 270�), the bearing is equal to the azimuth minus 180�. When the azimuth is in the fourth quadrant (270� to 360�), the bearing is equal to 360� minus the azimuth. Since the numerical values of the bearings repeat in each quadrant, the bearings must be labeled to indicate which quadrant they are in. The label must indicate whether the bearing angle is measured from the north or south line and whether it is east or west of that line. For example, a line with an azimuth of 341�12�30" falls in the fourth or northwest (NW) quadrant and its bearing is N 18�47�30" W.
6-24. If the coordinate of a point and the azimuth and distance from that point to a second point are known, the coordinate of the second point can be computed. The azimuth and distance from Station A to Station B are determined by measuring the horizontal angle from the azimuth mark to Station B and the distance from Station A to Station B.
6-25. A grid is a rectangular system with the easting and the northing lines forming right angles at the point of intersection. The computation of the difference in northing (dN) (side Y) and the difference in easting (dE) (side X) requires the computation of a right triangle. The distance from Station A to Station B is the hypotenuse of the triangle, and the bearing angle (azimuth) is the known angle. The following formulas are used to compute dN and dE:
dN = cos azimuth x distance
dE = sin azimuth x distance
6-26. If the traverse leg falls in the first (northeast [NE]) quadrant, the value of the easting increases as the line goes east and the value of the northing increases as it goes north. The product of the dE and the dN are positive and are added to the easting and northing of Station A to obtain the coordinate of Station B.
6-27. When using trigonometric calculators to compute a traverse, enter the azimuth angle, and the calculator will provide the correct sign of the function and the dN and the dE. If the functions are taken from tables, the computer provides the sign of the function based on the quadrant. Lines going north have positive dNs; lines going south have negative dNs. Lines going east have positive dEs; lines going west have negative dEs.
6-28. The following are examples of how to determine the dN and the dE:
- Given an azimuth from Station A to Station B of 70�15�15" and a distance of 568.78 meters (this falls in the first [NE] quadrant), compute the dN and the dE.
dN = cos 70�15�15" x 568.78 = +0.337848 x 568.78 = +192.16 m
dE = sin 70�15�15" x 568.78 = +0.941200 x 568.78 = +535.34 m- Given an azimuth from Station B to Station C of 161�12�30" and a distance of 548.74 meters (this falls in the second [southeast] [SE] quadrant), compute the dN and the dE.
dN = cos 161�12�30" x 548.74 = -0.946696 x 548.74 = -519.49 m
dE = sin 161�12�30" x 548.74 = +0.322128 x 548.74 = +176.76 m- Given an azimuth from Station C to Station A of 294�40�45" and a distance of 783.74 meters (this falls in the fourth [NW] quadrant), compute the dN and the dE.
dN = cos 294�40�45" x 783.74 = +0.417537 x 783.74 = +327.24 m
dE = sin 294�40�45" x 783.74 = -0.908660 x 783.74 = -712.15 m
6-29. The overall accuracy of a traverse depends on the equipment, the procedures used in the measurements, the accuracy achieved, and the accuracy of the starting and closing data. An accuracy ratio or ratio of closure (RC) of 1:5,000 is the minimum accuracy sought in topographic surveying. In obtaining horizontal distances, an accuracy of at least 2 millimeters per 100 meters must be obtained. When using a 1" theodolite, turn the horizontal angles four positions. Keep an angular closure of 10" per station.
SEA-LEVEL COEFFICIENT6-30. The corrected field distances must be reduced to sea level. Along any traverse with variations in elevation not exceeding 300 meters, sufficient accuracy may be obtained by computing a sea-level coefficient (SLC) for the entire traverse.
LINEAR ERROR6-31. To determine the acceptability of a traverse, compute the linear error of closure (LEC) (using the Pythagorean theorem), the AE, and the accuracy ratio. The first step in a closed-traverse case is to determine the linear error in the dN and the dE. In the case of a loop traverse, the algebraic sum of the dNs and the dEs should equal zero. Any discrepancy is the linear error in the dN or the dE.
AE6-32. The AE should then be computed using the appropriate accuracy ratio (1:5,000 or better) and the total length of the traverse. Compare this to the LEC. If the AE is greater than the LEC, the traverse is good and can be adjusted. If the traverse is not good, it must be redone.
RC6-33. The RC determines the traverse accuracy and compares it to established standards. The RC is the ratio of the LEC (after it is reduced to a common ratio and rounded down) to the total length of the traverse. If the RC does not fall within allowable limits, the traverse must be redone. It is very possible that the measured distances are correct and that the error can be attributed to large, compensating angular errors.
6-34. The accuracy of a traverse is the ratio of error to the total length of the traverse. The RC must meet the specifications for the order of work being performed. Third-order, Class I accuracy requires an RC of 1:10,000. Accuracy requirements are identified in DMS ST 031. If the traverse does not meet this specification, no further computations are necessary.
COORDINATE ADJUSTMENT6-35. Make the adjustment of the traverse using the compass rule. This rule states that for any leg of the traverse, the correction to be given to the dN or the dE is to the total correction for the dN or the dE as the length of the leg is to the total length of the traverse. The total correction for the dN or the dE is numerically equal to the error in northing (En) or the error in easting (Ee), but with the opposite sign.
6-36. When adjusting a traverse that starts and ends on two different stations, compute the coordinates before the error is determined. The correction (per leg) is determined in the same manner, but it is applied directly to the coordinates. The correction to be applied after computing the first leg is equal to the correction computed for the first leg. The correction to be applied after computing the second leg is equal to the correction computed for the first leg plus the correction computed for the second leg. The correction for the third leg equals the correction computed for the first leg plus the correction computed for the second leg plus the correction computed for the third leg and so on throughout the traverse. The final correction must be equal to the total correction required.